XY-Wing

An den folgenden Beispielen möchten wir Ihnen eine Situation erläutern, in der wir die Sudokustrategie des XY-Wing anwenden.

Die schwarzen Zahlen sind die ursprünglich vorgegebenen. Die blauen Zahlen haben wir durch die Anwendung einfacher oder auch schon fortgeschrittener Techniken gefunden. Die kleinen Zahlen stehen für die noch verbleibenden Möglichkeiten, es sind die so genannten Kandidaten. (Im vorliegenden Beispiele können diese bereits durch den Einsatz anderer, fortgeschrittener Techniken weiter reduziert worden sein.)

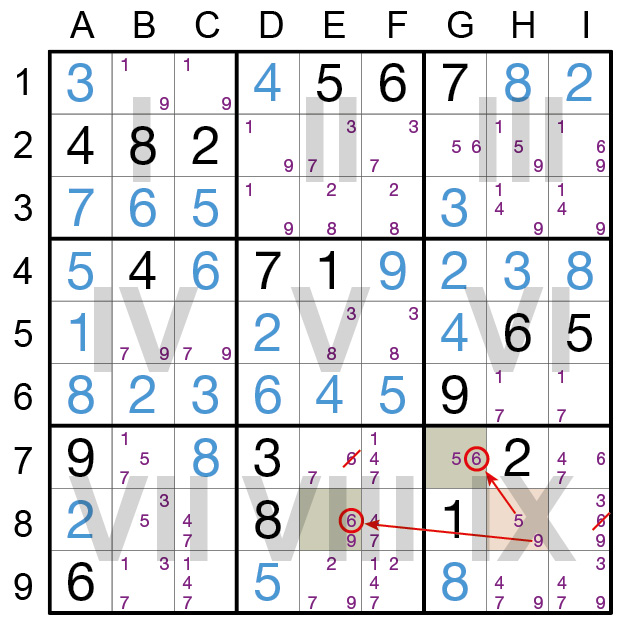
Das XY-Wing spielt sich in zwei sich überschneidenden Einheiten (hier: Zeile 8 und Block IX) ab. Findet man dort drei Felder mit je nur zwei Kandidaten (hier farbig hervorgehoben) aus insgesamt nur drei verschiedenen Kandidaten werten (hier: 5, 6 und 9), und sind alle drei Pärchen verschieden, so kann man mit diesen drei Pärchen in diesen beiden sich überschneidenden Einheiten eine Kette bilden, wobei die beiden Enden (hier: grün) stets einen gemeinsamen Kandidaten (hier: 6) aufweisen. Unabhängig davon, welcher der beiden Kandidaten im mittleren Kettenfeld (hier: orange) der richtige ist: Einer der beiden Vertreter des gemeinsamen Kandidatenwerts (hier: 6) ist der richtige. Die logische Folge ist: Im gemeinsamen Wirkungsbereich, also im Schnittpunkt der beiden Endfelder (hier: F7) und im Überlappungsbereich aus Reihe (hier: Zeile 8) und Block (hier: Block IX), können alle weiteren Vertreter dieses Kandidatenwerts gestrichen werden (hier: die beiden 6en in E7 und I8).

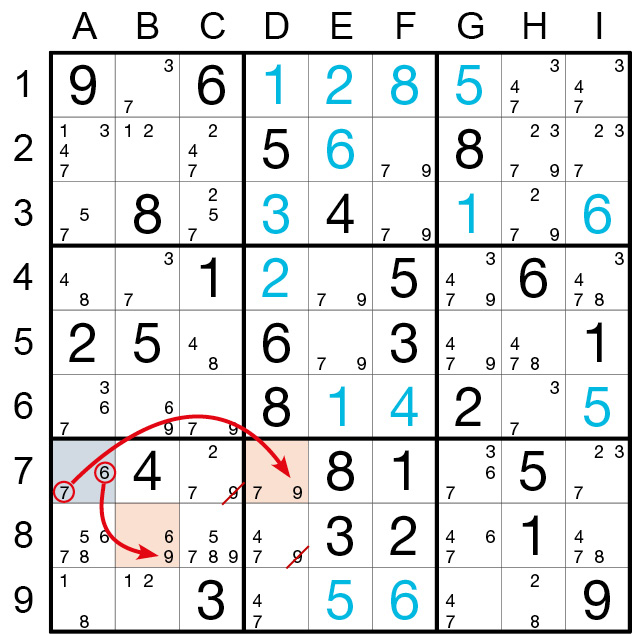
Der XY-Wing im nächsten Anschauungsbeispiel wird aus drei unterschiedlichen Kandidatenpärchen gebildet (hier: 6,7, 6,9 und 7,9), wobei die Kandidaten insgesamt drei Werte (hier: 6, 7 und 9) aufweisen. Die drei betroffenen Felder liegen in zwei sich überschneidenden Einheiten (hier: Zeile 7 und Block 7). Solch eine Anordnung bildet stets eine logische Kette, die dazu führt, dass der gemeinsame Kandidatenwert (hier: 9) der beiden Kettenenden (hier: D7 und B8) im Überschneidungsbereich dieser beiden Kettenenden entfernt werden kann.

Was in der sprachlichen Beschreibung sehr abstrakt und schwer verständlich wirkt, ist in der konkreten Darstellung unten leicht nachzuvollziehen. Probieren Sie gedanklich die beiden Möglichkeiten innerhalb der drei relevanten Felder durch.