XY-Kette

Am folgenden Beispiel möchten wir Ihnen eine Situation erläutern, in der wir die Sudokustrategie der XY-Kette anwenden.

Die schwarzen Zahlen sind die ursprünglich vorgegebenen. Die blauen Zahlen haben wir durch die Anwendung einfacher oder auch schon fortgeschrittener Techniken gefunden. Die kleinen Zahlen stehen für die noch verbleibenden Möglichkeiten, es sind die so genannten Kandidaten. (Im vorliegenden Beispiele können diese bereits durch den Einsatz anderer, fortgeschrittener Techniken weiter reduziert worden sein.)

Das Prinzip der XY-Kette ist – wie bei den meisten Lösungsstrategien – einfach: Es existieren zwei Möglichkeiten; beide führen zum selben Ergebnis. Die XY-Kette hat ein Startfeld mit zwei Kandidaten, und beide Kandidaten initiieren einen logischen Weg, der in beiden Fällen auf den selben Kandidatenwert endet. Im logischen Überschneidungsbereich dieser beiden Endfelder (dort, wo sich beide Endfelder der XY-Kette auswirken) können die Kandidaten dieses Werts eliminiert werden.

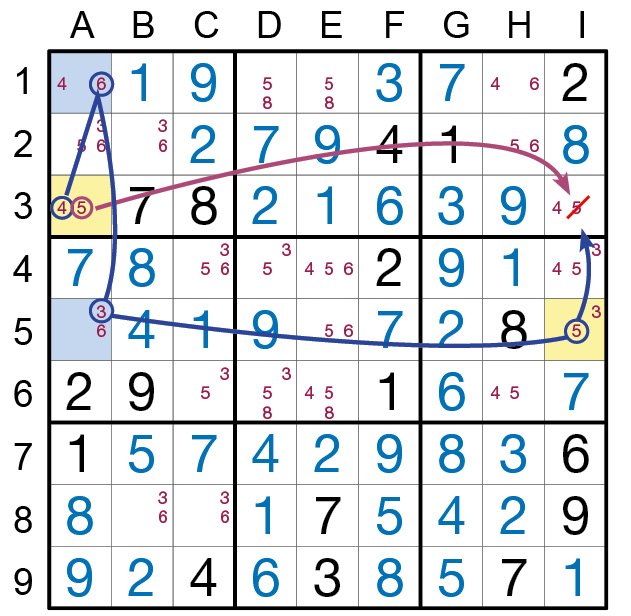
Im Beispiel erkennen wir im Kästchen A3 das Startfeld dieser Strategie. Von hier aus gibt es zwei Möglichkeiten: Wäre die 5 die gesuchte Zahl, so wirkte sich dies direkt auf das Zielfeld I3 aus (roter Pfeil), und man könnte diesen Wert im Zielfeld streichen. (Dieser Kettenteil besteht aus nur einem Feld). Wäre andernfalls die 4 die richtige Zahl, so käme es über zwingende, kettenartige Verknüpfungen (wie es der blaue Pfeilverlauf darstellt) ebenfalls zur selben Streichung. Auch wenn wir noch nicht wissen, welche der beiden Kandidaten in A3 die gesuchte Zahl ist, können wir den Kandidaten 5 in I3 (wie dargestellt) streichen.

Eine XY-Kette gehört zu den schwer zu findenden Strategien – vor allem, wenn sie noch länger ist als die im Beispiel. Aus nur drei Kettengliedern bestehend wäre sie übrigens ein XY-Wing. (Der XY-Wing wird an anderer Stelle erklärt.)