Lösungsstrategien Teil 3 (für Profis)
21. XY-Wing
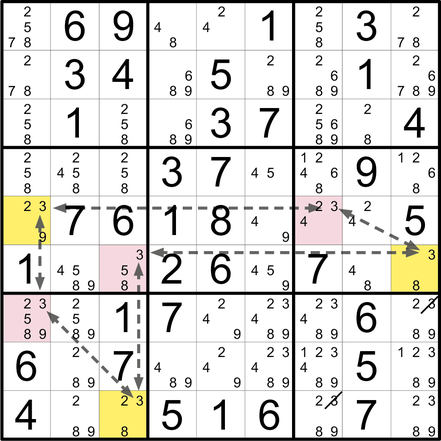
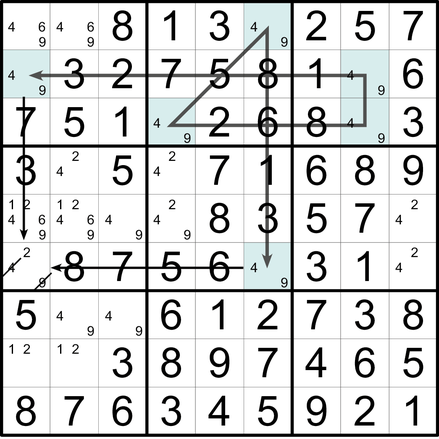
Diese Technik ist nicht mit dem X-Wing verwandt. Es ist eher ein Nackter Dreier in Kettenfunktion. Es geht um drei Kandidaten (hier: 4, 5 und 7), die in drei Feldern drei unterschiedliche Paare bilden (und in diesen Feldern allein sind) und dabei einen kettenartigen Zusammenhang aufweisen. Diese drei Felder müssen sich dafür in zwei sich überlagernden Einheiten befinden (hier: Z1 und B2). Die beiden Enden dieser Kette haben immer einen gemeinsamen Kandidaten (hier: 5). Kandidaten dieses Werts können im gemeinsamen Einflussbereich der beiden Endfelder (dicker Rahmen) eliminiert werden.
22. XYZ-Wing
Innerhalb eines Blocks (hier: B4) und einer Reihe (hier: Z4) gibt es drei Felder (hier: türkis) mit insgesamt drei verschiedenen Kandidaten (hier: 2, 5 und 9), die folgende Eigenschaften haben: Einer dieser Kandidaten ist in allen drei Feldern enthalten (hier: die 2), in zwei Feldern befinden sich zwei unterschiedliche Kandidatenpaare (hier: 2,5 und 2,9), und in einem Kästchen befinden sich alle drei Kandidaten, wobei dieses Kästchen im Schnittbereich des Blocks und der Reihe liegt (dicker Rahmen). Kandidaten mit dem Wert des gemeinsamen Kandidaten (hier: 2) können im genannten Schnittbereich gestrichen werden.
23. X-Kette
Gibt es in einer Einheit nur zwei Kandidaten eines Werts, so ist immer einer davon der richtige und der andere falsch. Findet man mehrere solcher Kandidatenpaare eines bestimmten Werts (hier: 3) und überschneiden sich deren Einheiten, so lassen sich logische Ketten bilden, in denen die Kandidaten abwechselnd wahr oder falsch sind. In den Feldern, die im Einflussbereich eines »wahren« und eines »falschen« Felds liegen, kann der Kandidat gestrichen werden.
24. XY-Kette
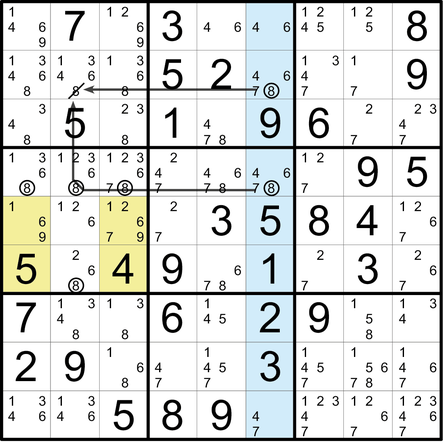
Die XY-Kette ist ein um mindestens ein Kettenglied erweitertes XY-Wing. Diese Kette (hier: gelbe Felder, Enden in Z1S6 und Z2S1) hat ein Startfeld (Z2S8) und endet in beide Richtungen auf derselben Zahl (hier: 1). Daher können im Einflussbereich der beiden Endfelder die Kandidaten dieses Werts (hier: 1) gestrichen werden.
25. Schwertfisch mit Flosse
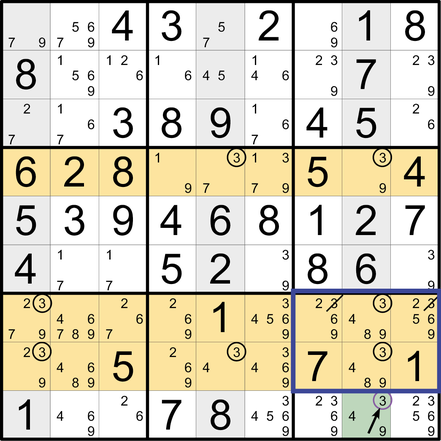
Sie sehen im Beispiel einen Schwertfisch (hier: aus 3en), der durch einen weiteren Kandidaten (»Flosse«, Pfeil) gestört wird – es ist damit kein richtiger Schwertfisch. Dennoch kann man diese Variante nutzen: Im Überschneidungsbereich, wo sich sowohl die Flosse als auch der klassische Schwertfisch auswirken (blauer Rahmen), können die Kandidaten dieses Werts eliminiert werden.
26. W-Wing
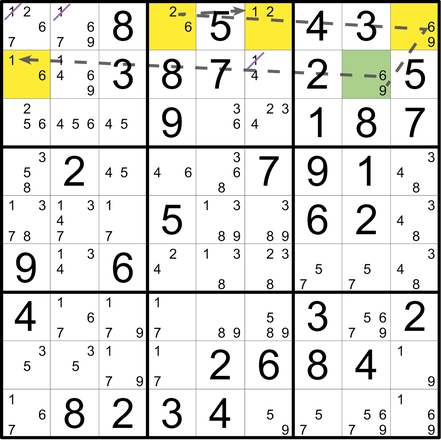
Zwei Felder enthalten ausschließlich die gleichen beiden Kandidaten (hier: 6 und 8 in Z2S1 und Z6S5. Diese beiden Felder bilden die Endpunkte eines imaginären Ws.). Das zweite Konstellationsmerkmal ist eine Reihe (hier: Z8), die einen der beiden genannten Kandidaten genau zweimal enthält (hier: die 6), und zwar jeweils auf Höhe der beiden »W-Endpunkte«. Nun kann im Überschneidungsbereich dieser W-Endpunkte (hier: im Feld Z6S1, die mittlere Spitze des Ws) der andere der beiden Kandidaten (hier: 8) eliminiert werden. Probieren Sie’s aus: Auch falls die 6 in einem der grünen Felder die richtige Zahl wäre, führte dies jeweils zur hier dargestellten Streichung der 8.)
27. Geklonte Paare
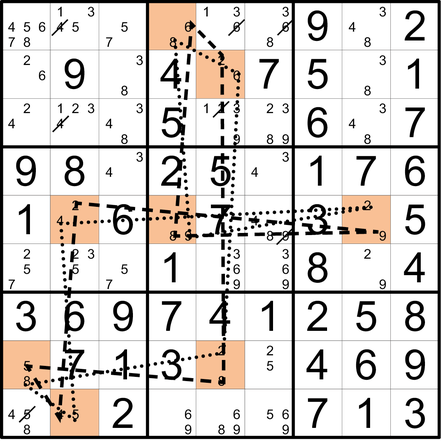
Lässt sich mit mehreren identischen Nackten Paaren (hier: 4/9) eine mindestens vier Kästchen umfassende Kette (mindestens drei logische Schritte) bilden, dann lassen sich alle Kandidaten dieser beiden Werte streichen, die sich im Einflussbereich zweier Kettenfelder befinden, die einen Abstand von mindestens 3 oder einer anderen, ungeraden Anzahl an Schritten aufweisen.
28. Leeres Rechteck
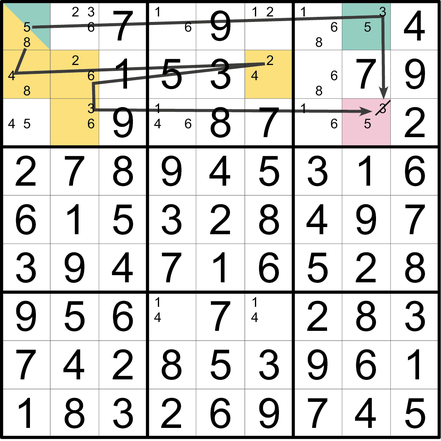
Das Leere Rechteck wird aus vier im Rechteck angeordneten Feldern innerhalb eines Blocks gebildet (hier: die hellgrünen Felder in B4). Es bedeutet, dass in diesen vier Feldern keine Kandidaten eines bestimmten Werts (hier: 8) enthalten sind, während sowohl die diesen Block durchquerende Zeile als auch die Spalte (beide führen am Leeren Rechteck vorbei) je mindestens einen separaten Kandidaten dieses Werts aufweisen. Diese Konstellation hat die Funktion einer Wirkungsumleitung. (So viel zum namensgebenden Element dieser Strategie.)
Logischer Ausgangspunkt der Anwendung ist eine Reihe, die nur zwei Kandidaten eines Werts enthält (hier: 8 in S6). Einer dieser Kandidaten (hier: Z2S6) würde sich direkt über die quer verlaufende Reihe (hier: Z2) auf das Zielfeld (hier: Z2S2) auswirken. Der andere Kandidat (hier: Z4S6) würde sich über die Umlenkung des Leeren Rechtecks ebenfalls auf das Zielfeld (hier: Z2S2) auswirken.
29. Doppelkette
Hier lassen sich zwei geschlossene Ketten (ohne Anfang und Ende) auf denselben Feldern bilden. Kommt nun ein Wert in dieser Kette innerhalb einer Einheit zweimal vor, so kann man schließen, dass einer davon die richtige Zahl sein muss. Alle anderen Kandidaten dieses Werts in dieser Einheit können daher gestrichen werden.
30. Forcing Chain
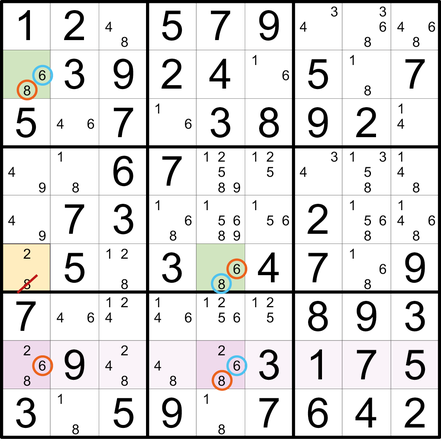
Zwei als letzte im Feld verbliebene Kandidaten (hier: 5 und 8 im zweifarbigen Startfeld) führen über zwei dominokettenartig verknüpfte Wege zur selben Streichung (hier: die 3 in Z3S8). Das heißt, die 3 im Zielfeld wird in jedem Fall gestrichen, egal, welche Zahl im Startfeld die richtige ist.