Verbotenes Rechteck Typ 3

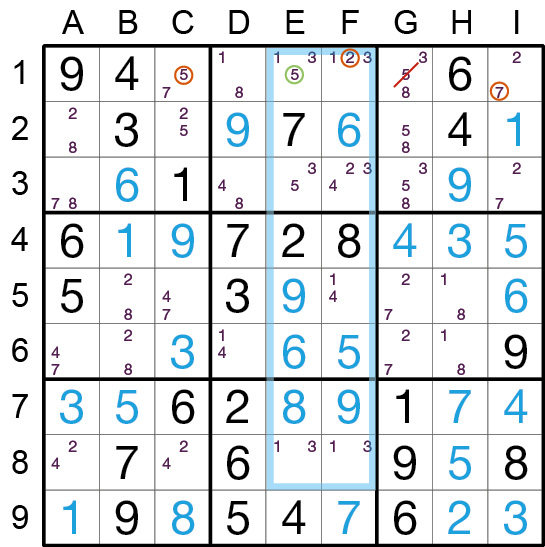
Am folgenden Beispiel möchten wir Ihnen eine Situation erläutern, in der wir die Sudokustrategie des Verbotenen Rechtecks vom Typ 3 anwenden.

Die schwarzen Zahlen sind die ursprünglich vorgegebenen. Die blauen Zahlen haben wir durch die Anwendung einfacher oder auch schon fortgeschrittener Techniken gefunden. Die kleinen Zahlen stehen für die noch verbleibenden Möglichkeiten, es sind die so genannten Kandidaten. (Im vorliegenden Beispiele können diese bereits durch den Einsatz anderer, fortgeschrittener Techniken weiter reduziert worden sein.)

Worauf wir uns dieses Mal konzentrieren wollen, ist eine Konstellation, die den Einsatz der Lösungstechnik "Verbotenes Rechteck vom Typ 3" erlaubt. Die logische Grundlage dieser Strategie ist die Vorgabe, dass Sudokus generell nur eine einzige Lösung haben.
Würden vier im Rechteck angeordnete Kästchen lediglich dieselben zwei Kandidaten enthalten, wäre das Sudoku nicht eindeutig. Daher kann man folgende Regel schließen: Gibt es unter den vier Feldern eines solchen Verbotenen Rechtecks zwei Felder, die zwei oder mehr weitere Kandidaten enthalten, und befinden sich diese beiden Felder innerhalb einer Einheit (Zeile, Spalte oder Block), so muss einer dieser anderen Kandidaten (in unserem Fall eine 2 oder eine 5) die richtige Zahl sein. Beim Typ 3 des Verbotenen Rechtecks finden wir eine Konstellation vor, bei der es zu Streichungen von Kandidaten außerhalb dieser vier Felder des Rechtecks kommt. Betrachten Sie den Fall unten: Ob nun die 2 oder die 5 (innerhalb des Verbotenen Rechtecks) die richtige Zahl ist, wissen wir nicht. In beiden Fällen jedoch bewirken logischen Zusammenhänge mit anderen Feldern, dass es zur dargestellten Streichung kommt. Denn wäre die rot eingekreiste 2 in Feld F1 die richtige Zahl, dann müsste in I1 die 7 und in C1 die 5 stehen. ebenso wie die 5 in E1 bewirkt dies also die Eliminierung der 5 in G1.