Steinbutt

Am folgenden Beispiel möchten wir Ihnen eine Situation erläutern, in der wir die Sudokustrategie des Steinbutts anwenden (übrigens verwandt mit den Strategien "Drachen" und "Wolkenkratzer").

Die schwarzen Zahlen sind die ursprünglich vorgegebenen. Die blauen Zahlen haben wir durch die Anwendung einfacher oder auch schon fortgeschrittener Techniken gefunden. Die kleinen Zahlen stehen für die noch verbleibenden Möglichkeiten, es sind die so genannten Kandidaten. (Im vorliegenden Beispiele können diese bereits durch den Einsatz anderer, fortgeschrittener Techniken weiter reduziert worden sein.)

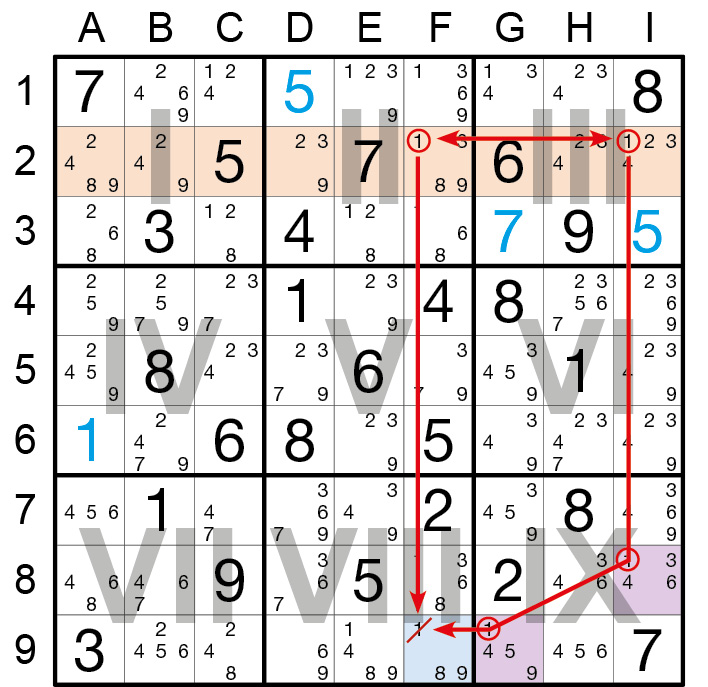
Der Steinbutt bildet äußerlich betrachtet eine Schleife über fünf Felder, deren Form der Technik ihren Namen gab. Der gedankliche Ausgangspunkt ist eine Reihe, in der Kandidaten eines Werts nur zweimal vorkommen (hier: Kandidat 1 in Zeile 2). Das Zielobjekt befindet sich in einem Feld, das von beiden dieser Ausgangskandidaten im logischen Sinne erreicht wird (hier: Kandidat 1 im blauen Feld 9F). Unabhängig davon, welcher der beiden Kandidaten in der Ausgangsreihe der richtige ist, können wir den betreffenden Kandidaten im Zielfeld eliminieren.
Gehen wir dies einmal anhand unseres Beispiels praktisch durch – es ist im Grunde einfach: Wäre die 1 im Feld 2F die richtige Zahl, würde man die 1 in Feld 9F streichen (und auch weitere 1en in den betroffenen Einheiten Zeile, Spalte, Unterquadrat). Nun kommt das Besondere am Steinbutt: Die andere 1 in Zeile 2 wirkt sich über zwei Zwischenschritte im Unterquadrat IX ebenfalls auf das Feld 9F aus. Wäre nämlich die 1 in 2I die richtige, dann müsste man die 1 in 8I streichen. Dann wiederum wäre die zweite 1 in diesem Unterquadrat  (in 9G) die richtige Zahl, was schließlich ebenfalls zur Streichung der 1 in Feld 9F führte.

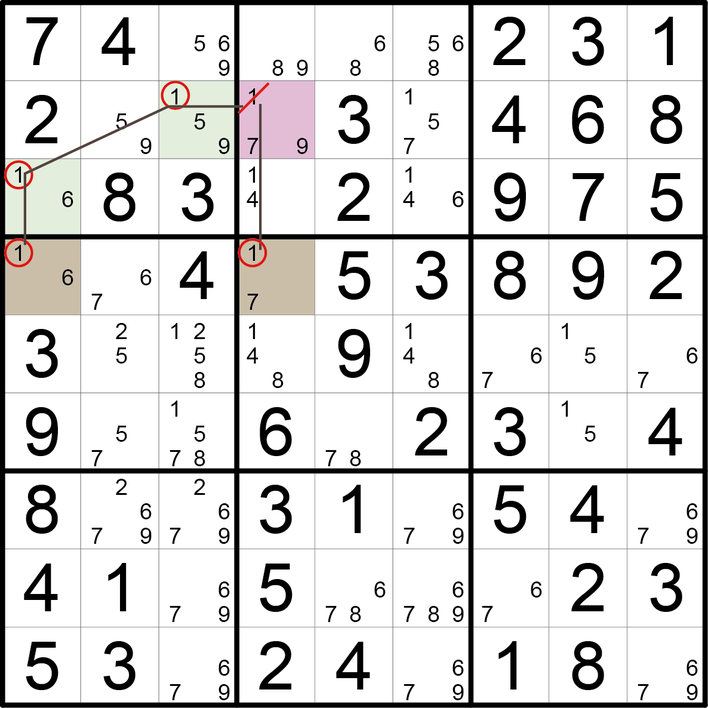
Weiteres Beispiel für den Einsatz eines Steinbutts:

Ein Steinbutt wird immer in vier im Rechteck angeordneten Blöcken gebildet. In einer Reihe (hier: Z4) kommt ein Kandidat (hier: 1) genau zweimal vor. Egal, welcher dieser beiden der Richtige ist, kommt es entweder direkt (orthogonale Reihe, hier: S4) oder über eine kleine Dominokette (hier: linker fraglicher Kandidat 1 wirkt sich über B1 – die „Schwanzflosse“ des Steinbutts – auf dasselbe rosa Feld aus) zur Streichung dieses Kandidaten im logischen Kreuzungspunkt (hier: rosa Feld).