Lösungsstrategien Teil 2 (für Profis)
11. X-Wing
Existiert ein Kandidatenwert (hier: 8) in zwei Zeilen (hier: Z5 und Z9) in jeweils nur zwei Feldern, und liegen diese vier Felder in nur zwei Spalten (hier: S3 und S6), dann können alle weiteren Kandidaten dieses Werts aus diesen beiden Spalten entfernt werden (da nur möglich: Z5S3 + Z9S6 ODER Z5S6 + Z9S3).
Dieses Prinzip gilt natürlich auch umgekehrt für Spalten, die jeweils nur zwei Kandidaten eines Werts enthalten.
12. Steinbutt
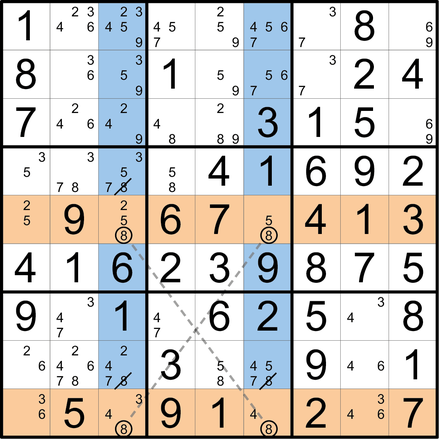
In einer Reihe (hier: Z3) kommt ein Kandidat nur zweimal in verschiedenen Blöcken vor. Egal, welcher der Richtige ist, kommt es entweder direkt (orthogonale Reihe, linker Pfeil) oder über eine kleine Dominokette (rechter Pfeilverlauf) zur Streichung eines Kandidaten dieses Werts in einem korrespondierenden Block.
13. Drittes Auge
Im ganzen Rätsel weisen alle noch leeren Felder nur noch zwei Kandidaten auf - bis auf ein Feld mit drei Kandidaten (hier: Z1S2). Derjenige Kandidatenwert in diesem Feld, der dreimal in der Einheit enthalten ist, ist zwingend die richtige Zahl (hier: 7). Andernfalls (falls diese 7 gestrichen würde) wäre das Sudoku nicht eindeutig.
14. Wolkenkratzer
Es existieren zwei parallele Reihen (hier: S4 und S8), die jeweils genau zweimal denselben Kandidaten aufweisen (hier: 2), wobei ein Kandidat der einen Reihe mit einem Kandidaten der anderen Reihe auf gleicher Höhe (hier: in Z9) liegt. Eliminiert werden können nun die Kandidaten gleichen Werts, die im gemeinsamen Einflussbereich (hier: graue Umrahmung) der beiden anderen Kandidaten aus Z4S4 und Z5S8 liegen. In der Konstellation des Wolkenkratzers ist zumindest einer der beiden versetzt gegenüberliegenden Kandidaten der Richtige.
15. Schwertfisch
Der Schwertfisch ist eine Erweiterung des X-Wings. Liegen in genau drei Spalten (hier: S3, S6 und S9) alle Kandidaten eines Werts (hier: 9) in genau drei Zeilen (hier: Z5, Z6 und Z9), dann befindet sich die Lösungskombination des genannten Werts (hier: 9) irgendwo in den Schnittpunkten dieser drei Zeilen mit den drei Spalten. Letztlich teilen sich also drei Zahlen dieses Kandidatenwerts (hier also drei 9en) diese drei Zeilen und Spalten in den in Frage kommenden Schnittpunkten untereinander auf. Alle anderen Kandidaten dieses Werts können somit in den betroffenen Zeilen gestrichen werden.
Dieses Prinzip gilt natürlich auch umgekehrt für drei Zeilen, die jeweils nur drei Kandidaten eines Werts enthalten.
16. Drachen
Ein Kandidatenwert (hier: 6) existiert in einer Zeile (hier: Z5) und einer Spalte (hier S9) je nur zweimal. Befindet sich je ein Kandidat dieser beiden Paare in einem gemeinsamen Block (hier: Block 6), kann dieser Wert im Schnittpunkt der beiden anderen Kandidaten (hier: Z7S2) eliminiert werden.
17. Verbotenes Rechteck Typ 1
Sudokus dürfen vom Grundsatz her nur eine einzige Lösung haben. Würden vier im Rechteck angeordnete Felder ausschließlich dieselben zwei Kandidaten enthalten (hier: 4 und 5 in den vier violetten Feldern), ginge das nur auf, wenn mehrere Lösungen existierten. Da wir aber wissen, dass ein Sudoku nur eine Lösung hat, kann diese Möglichkeit nicht stimmen. In dem Feld, das noch weitere Kandidaten enthält (hier: Z8S7), müssen daher die beiden »verbotenen« Kandidaten entfernt werden.
18. Verbotenes Rechteck Typ 2
Diese Strategie basiert auf derselben logischen Grundlage wie das Verbotene Rechteck Typ 1. Beim Typ 2 jedoch enthalten zwei der vier Felder dieses Rechtecks (hier: Z2S1 und Z3S1), die zudem innerhalb einer Einheit (hier: S1 bzw. B1) liegen, einen dritten, jeweils gleichen Kandidaten (hier: 5). Einer dieser beiden Kandidaten muss die richtige Zahl sein. Deshalb eliminieren wir alle anderen Kandidaten dieses Werts in den betroffenen Einheiten (hier: B1 und S1).
19. Verbotenes Rechteck Typ 3
Dieser Typ ist relativ kompliziert, da er viele Möglichkeiten bietet und schwer zu entdecken ist. Entscheidend ist, dass wir das Prinzip des Verbotenen Rechtecks generell verstehen und wissen, dass in mindestens einem Feld des Verbotenen Rechtecks eine andere Zahl als die beiden betroffenen Kandidaten (hier: 4 und 6) stehen muss.
Im vorliegenden Fall würde also mindestens in einem der Felder Z1S2 und Z3S2 die 5 oder die 8 gesetzt werden. Unabhängig davon, welche letztendlich die richtige Zahl ist, führen alle vier Möglichkeiten in diesem Fall (5 oder 8 in Feld Z1S2 oder Z3S2) zu denselben drei dargestellten Streichungen.
20. Verbotenes Rechteck Typ 4
In zwei Feldern eines Verbotenen Rechtecks (hier: Z4S2 und Z6S2) befinden sich zusätzliche Kandidaten, und unter den beiden »verbotenen« Kandidatenwerten (hier: 1 und 5) in diesen beiden Feldern ist ein Wert (hier: 1), der in keinen anderen Feldern der betroffenen Einheiten S2 bzw. B4 vorkommt. Einer dieser beiden Kandidaten (hier: 1) muss daher die richtige Zahl sein. Folglich wird in diesen Feldern der andere »verbotene« Kandidat (hier: 5) ausgemustert.