Logikrätsel
Das populärste Logikrätsel trägt zweifelsohne den Namen Sudoku. Doch echte Logikfans geben sich mit nur einer Rätselart natürlich nicht zufrieden. Neben vielen Sudoku-Varianten gibt es eine unüberschaubare Menge an Logikrätsel-Arten, die Freunde des korrekten Schließens regelmäßig einen Flow bescheren. Hervorzuheben aus der Masse wären noch die klassischen "Hinweise"-Logicals und unser Eigengewächs namens "Snords", die es u. a. durch die Magazine P.M. Logik-Trainer und P.M. Snords zu größerer Bekanntheit in Deutschland gebracht haben.
Gartenzaun
Zeichnen Sie in das Diagramm einen geschlossenen Zaun, der entlang der Punkte und feinen Linien verläuft. Dieser darf sich an keiner Stelle berühren
oder schneiden. Die Zahlen in den Kästchen geben an, wie viele Zaunstücke an dieses Kästchen grenzen.
Kakuro
Die kleinen Zahlen in den Kästchen zeigen die jeweilige Summe der Zahlen in der Reihe von freien Feldern rechts davon bzw. darunter an. Dabei gilt:
• Es dürfen nur die Ziffern von 1 bis 9 vorkommen
• In jeder Summe darf jede Ziffer nur einmal vorkommen
• In jedes freie Feld darf nur eine Ziffer eingetragen werden
Cropurec
Hier soll ein vollständiges Kreuzworträtsel wiederhergestellt werden. Dieses wurde in 15 Quadrate zu je neun Kästchen zerlegt – diese Quadrate sind in gemischter Anordnung im oberen Teil des Rätsels dargestellt. Alle Buchstaben und die schwarzen Blindfelder sind durch Zahlen ersetzt, wobei eine feste Zuordnung besteht. In der Zuordnungstabelle rechts sind bereits einige Eintragungen gemacht. Auch stehen einige Buchstaben und Blindfelder des ursprünglichen Rätsels bereits an Ort und Stelle. Nutzen Sie die Hinweise unten.
Münzsammler
Gehen Sie von A nach B und sammeln Sie dabei alle Goldstücke auf. Bewegen Sie sich ausschließlich in horizontale oder vertikale Richtung. Ihr Weg darf sich niemals kreuzen oder auch nur berühren (auch nicht an diagonal benachbarten Eckpunkten).
Dominofeld
Die Felder unten bestehen aus jeweils 56 kleinen Quadraten. Je zwei davon bilden einen Dominostein – das Problem ist nur, dass die Ränder der einzelnen Steine nicht zu sehen sind. Sämtliche 28 Kombinationen (0-0, 0-1, 0-2, … 6-6) sind enthalten, sodass jeder Dominostein eine andere Zahlenkombination hat. Finden Sie heraus, wie die Steine liegen bzw. wo die Ränder der einzelnen Steine sind, und zeichnen Sie diese ein.
Zahlengeflecht
In die leeren Felder sollen die Zahlen 1 bis 8 eingetragen werden. Jede Zahl ist mit anderen verbunden; wenn man die mit ihr verbundenen Zahlen zusammenzählt, ergibt sich die rechts vom Pfeil angegebene Summe. Welche Zahlen gehören also in die Kreise, damit die vorgegebenen Summen erreicht werden?
Futoshiki
Tragen Sie in die leeren Felder Zahlen von 1 bis 5 ein, sodass in jeder Zeile und Spalte jede davon genau einmal enthalten ist.
HexaLog
Die Zahlen in den grauen Sechsecken sind die Summen der Zahlen in weißen Feldern, die dieses Feld umgeben. Tragen Sie in die weißen Felder Zahlen von 1 bis 9 ein. Jede Zahl darf nur einmal dasselbe graue Feld berühren.
Dreiecksortung
Sechs Schiffe sind hier zu finden. Sie berühren sich an keiner Stelle, auch nicht an den Ecken. Den Zahlen am Rand können Sie entnehmen, wie viele Schiffsteile die jeweilige Reihe enthält.
Startzeichen
Tragen Sie die Buchstaben A, B, C und D je einmal in die weißen Felder jeder Zeile und Spalte ein. Aus den Buchstaben am Rand können Sie entnehmen, welcher Buchstabe in der jeweiligen Zeile bzw. Spalte den Anfang macht. Steht der Buchstabe am rechten oder am unteren Rand, so bedeutet das, dass er der erste Buchstabe von rechts bzw. von unten gesehen ist.
Picknick
Welche Zahl fehlt im leeren Kästchen?
FairCut
Trennen Sie diese Anordnung in sechs zusammenhängende Bereiche, sodass jedes der fünf Symbole in jedem Bereich einmal enthalten ist.
Magneto
Das Rätselfeld besteht aus lauter rechteckigen Platten; diese sind entweder magnetisch – haben also einen Nord- und einen Südpol, oder sie sind neutral. Magnetfelder haben bekanntlich die Eigenschaft, dass sich gegensätzliche Pole anziehen und gleichnamige Pole abstoßen.
Wo befinden sich die neutralen Platten?
Hexapath
Zeichnen Sie in das leere Gitter
unten eine Schleife zusammen-
hängender Sechsecke ein. Diese
Schleife darf keine scharfe Ecke
(Winkel kleiner als 90°) aufweisen. Die Zahlen geben an, durch wie viele der jeweils anliegenden Sechsecke der Weg verläuft. Die Zahlenfelder werden nicht durchlaufen.
Wachmännchen
An jedem Palastgebäude soll ein Wachmann stehen – entweder direkt neben, über oder unter dem Gebäude, also nicht diagonal dazu. Die Wächter dürfen nicht auf benachbarten Feldern stehen – dies gilt auch für diagonal angrenzende Felder. Die Zahlen am Rand bestimmen die Anzahl der Wachmänner in der jeweiligen Reihe beziehungsweise Spalte. Wo also müssen die Wächter postiert werden?
U-Boot-Jagd
Die Zahlen am Rand geben an, wie viele U-Boote sich in der jeweiligen Zeile beziehungsweise Spalte befinden. Jeder Pfeil zeigt dabei auf mindestens eins der gesuchten Objekte. Gleichfalls wird jedes U-Boot von mindestens einem Pfeil erreicht. Auf Feldern, auf denen ein Pfeil ist, befindet sich keines. Wo also befinden sich die fraglichen Objekte? Wenn Sie die Buchstaben der Lösungsfelder der Reihe nach verbinden, ergibt sich ein Lösungswort.
Lügentest 1
Wir wissen, dass genau zwei dieser drei fröhlichen Menschen ehrlich sind. Wer also lügt?
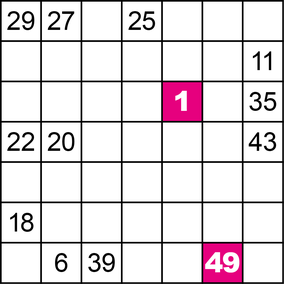
Black&White
Alle Zahlen von 1 bis 49 sollen in diesem Gitter genau einmal enthalten sein. Die entscheidende Regel ist, dass all diese Zahlen eine einzige Kette bilden, wobei die Felder (Kettenglieder) aufeinanderfolgender Zahlen direkt benachbart sein müssen (auch diagonal benachbart).
Diamanten
Unentdeckte Diamantvorkommen gilt es hier zu entdecken. Die Zahlen geben dabei an, wie viele
dieser Felder an das Kästchen
mit der jeweiligen Zahl grenzen
(waagrecht, senkrecht oder diagonal). Die Anzahl der zu findenden Diamantfelder ist 9.
Lügentest 2
Vier Frauen, unter ihnen auch Tina, sitzen an einem Tisch. Sie möchten gerne wissen, wie sie im einzelnen heißen, doch genau eine von ihnen lügt. Welchen Namen hat die Lügnerin?
Hidoku
Füllen Sie diese Gitter mit den Buchstaben B und W, wobei in allen Zeilen und Spalten gleich viele Bs wie Ws enthalten sein sollen. Dabei dürfen niemals mehr als zwei gleichlautende Buchstaben horizontal oder vertikal aufeinanderfolgen.
Blumenkinder
Zwei Mädchen pflücken auf einer Wiese in fünf Minuten zusammen 30 Blumen. Wie viele Blumen könnten fünf Mädchen in 30 Minuten pflücken?
Yahtzee
In den Feldern des Gitters sollen Augenzahlen eines Würfels stehen. Die Angaben rechts und unten zeigen für die jeweilige Zeile bzw. Spalte an, welche Yahtzee-Formation dabei die höchste Punktzahl erreicht. Zeichnen Sie die fehlenden Würfel ein.
Chess
Im Schachfeld halten sich auf den blauen Feldern sechs Figuren versteckt (ein König, eine Dame, ein Springer, ein Läufer, ein Turm und ein Bauer). Die Zahlen in den Feldern geben an, wie oft dieses Kästchen angegriffen wird. Können Sie herausfinden, welche der sechs Figuren sich jeweils auf welchem der blauen Felder befindet? (Die Spielrichtung des Bauern ist von unten nach oben.)