Lösungsstrategien Teil 1 (für Fortgeschrittene)
Das Beherrschen der Lösungsstrategien besitzt unter Sudokufreunden einen großen Stellenwert. Einfache Sudokus lassen sich meist noch intuitiv und durch konzentriertes Absuchen lösen. Die beiden dafür ausreichenden Anfängertechniken werden im Folgenden unter „Nackter Single“ und unter „Versteckter Single“ erläutert. Sie werden meist intuitiv und unbewusst eingesetzt, wenn für ein bestimmtes Feld nur eine Zahl möglich ist oder wenn eine bestimmte Zahl nur in ein einziges Feld passt. Bei kniffligeren Sudokus müssen gewissenhaft Notizen gemacht werden. Wir verwenden die Methode der „Kandidaten“. Mit ihr lassen sich die Zusammenhänge am besten beschreiben. Manche Situationen in einem anspruchsvollen Sudoku erfordern sehr komplexe Lösungsansätze. Diese leicht verständlich zu erklären ist eine Kunst für sich. Wir arbeiten daher mit grafischen Beispielen und hoffen, damit das Verständnis der behandelten Lösungstechniken zu erleichtern.
1. Versteckter Single
Jede bereits eingetragene Zahl deckt eine Zeile, eine Spalte und einen Block ab. Daher kommt es sehr oft zu Situationen, in denen es für eine bestimmte Zahl innerhalb einer Einheit* nur ein einziges freies Feld gibt (in Block 9 passt die 7 nur noch ins grüne Feld).
2. Nackter Single
Das gelbe Feld liegt im Einflussbereich (selbe Reihe** oder selber Block) von acht der neun möglichen Zahlen. Daher passt in dieses Kästchen nur noch eine Zahl (hier: 7).
Nackte Singles sind schwieriger zu entdecken als Versteckte, da hier jedes Kästchen einzeln untersucht werden muss.
3. Nacktes Paar
Besetzen die gleichen beiden Kandidatenwerte (hier: 2 und 4) zu zweit (also ohne andere Kandidaten) zwei Felder einer Einheit*, so teilen sie sich diese beiden Felder untereinander auf, und wir wissen zumindest, dass sie in den anderen Feldern dieser Einheit nicht weiter vorkommen können. Darum kann man diese beiden Werte im Rest der betroffenen Einheiten (hier: Zeile 3 und Block 2) entfernen.
4. Verstecktes Paar
Wenn zwei Kandidatenwerte (hier: 5 und 6) nur in zwei Feldern einer Einheit* vorhanden sind, kann man die anderen Kandidaten in diesen Feldern streichen, da diese zwei Kandidaten in keinen anderen Feldern dieser Einheit (hier: Zeile 4) sein können.
* Einheit = Zeile, Spalte oder Block - ** eine Reihe kann eine Zeile oder eine Spalte sein
5. Nackter Dreier
Existieren in drei Feldern einer Einheit ausschließlich und insgesamt nur drei verschiedene Kandidaten (hier: 1, 3 und 4), können diese in den übrigen Feldern dieser Einheit (hier: Z1) ausgesondert werden.
6. Versteckter Dreier
Wenn insgesamt drei unterschiedliche Kandidaten in genau drei Feldern einer Einheit vorkommen (hier: 4, 5 und 7), können alle anderen Kandidaten in diesen Feldern entfernt werden. (Existiert oft neben Nacktem Dreier.)
7. Nackter / Versteckter Vierer
Existieren in vier Feldern einer Einheit (hier: Block 7) ausschließlich und insgesamt nur vier verschiedene Kandidaten (hier: 4, 5, 6 und 8), können diese in den übrigen Feldern dieser Einheit ausgesondert werden.
Wenn insgesamt vier unterschiedliche Kandidaten in genau vier Feldern einer Einheit vorkommen (hier: 1, 2, 3 und 7), können alle anderen Kandidaten in diesen Feldern entfernt werden.
8. Reihe-Block-Check (RBC)
Befinden sich in einer Reihe (hier: Z4) alle Kandidaten einer Zahl (hier: 9) auch innerhalb nur eines Blocks (hier: B5), werden alle weiteren Kandidaten dieses Werts in diesem Block gestrichen.
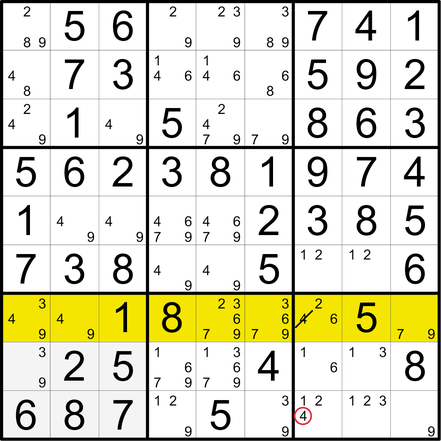
9. Block-Reihe-Check (BRC)
Liegen in einem Block (hier: B4) alle Kandidaten einer Zahl (hier: 8) in einer Reihe (hier: Z4), werden alle weiteren Kandidaten dieser Zahl aus dieser Reihe entfernt.
10. Erweiterter BRC
Diese Technik ist im Grunde die Kombination aus BRC und Verstecktem Single. Führt die durch ein BRC (hier: B7, Z7) bedingte Kandidateneliminierung (hier: eine 4 in B9) dazu, dass vom betroffenen Wert (hier: 4) nur noch ein Kandidat im Block (hier: Z9S7 in B9) übrig bleibt, so ist dieser die richtige Zahl.
