Sudokus
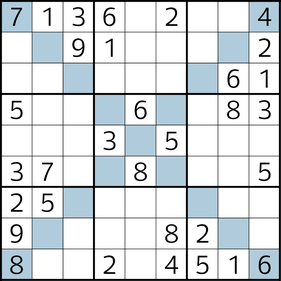
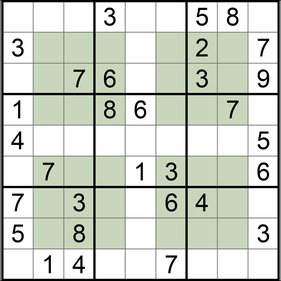
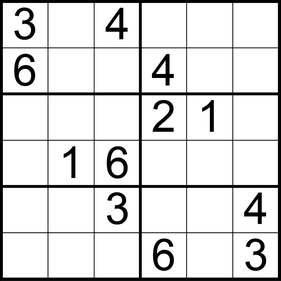
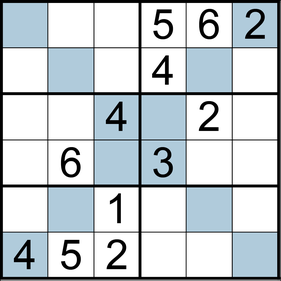
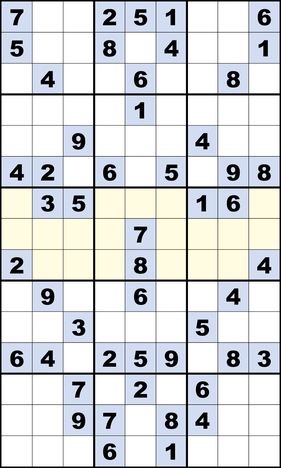
Sudoku is a strictly logical puzzle game in which you have to place numbers according to certain rules in a playing field. The goal is to fill in a 9x9 grid so that each unit (in the classic sudoku, this is a row, a column, and a 3x3 field block) will have all numbers from 1 to 9.
Why actually 1 to 9?
The fact that numbers are used in the sudokus is because we have a nice overview of the limited number of digits. However, arithmetic relationships between the numbers have no meaning. Sudoku works with everything that can be clearly identified: with letters, pictures, words, sounds, etc.
Determining the minimum number of constraints leading to a definite solution is an unsolved mathematical problem. At the moment, one assumes a minimum of 17 given numbers, which can represent a clear sudoku.
Sudoku
Fill in the grid field like this
that every number from 1 to 9 is contained in every row, in every column and in every 3 by 3 block exactly once.
Sudoku X
Additionally, in this sudoku variant, the numbers 1 through 9 are in each of the two main diagonals
must be included once (diagonal rule).
Form-Sudoku
Anstelle der Unterquadrate existieren hier unregelmäßig geformte Bereiche, die jeweils die Zahlen 1 bis 9 enthalten müssen
Hyper-Sudoku
Zusätzlich gilt hier, dass die Zahlen 1 bis 9 in jedem der vier gefärbten Innenblöcke je einmal enthalten sein müssen.
Kaiser-Sudoku
Neun ineinandergreifende Diagonal-Sudokus, die sich zwölf Blöcke (hier gelb) teilen
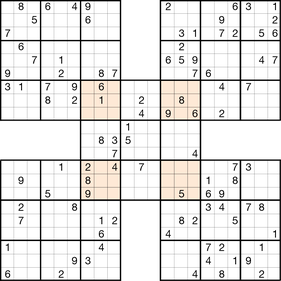
Stern-Sudoku
Hier müssen die Ziffern 1 bis 9 jeweils genau einmal in den fett umrandeten Dreiecken und in jeder Reihe bzw. Diagonalen vorkommen (gilt auch für die von der Sternmitte unterbrochenen Reihen), wobei die kürzere Reihe (am Rand) zusätzlich noch das Feld in den Sternecken verwendet.
Kreis-Sudoku
Hier müssen die Zahlen 1 bis 9 in jedem Ring, in jedem Strahl und in jedem dick eingefassten 3-x-3-Bereich genau einmal enthalten sein.
Killer-Sudoku
Innerhalb der gestrichelt umgrenzten Bereiche müssen die
einzutragenden Zahlen die vorgegebenen Summen ergeben.
Farb-Sudoku
Zusätzlich gilt hier, dass jeweils
alle neun Kästchen gleicher Farbe
die Zahlen 1 bis 9 genau einmal enthalten müssen
6er-Sudoku
Hier sollen die Zahlen 1 bis 6
eingetragen werden.
6er-Sudoku X
Hier sollen die Zahlen 1 bis 6
eingetragen werden. Bei entsprechenden farblichen Kennzeichnungen gilt zusätzlich die Diagonalenregel.
Samurai-Sudoku
Fünf ineinandergreifende Sudokus, die sich vier Unterquadrate teilen.
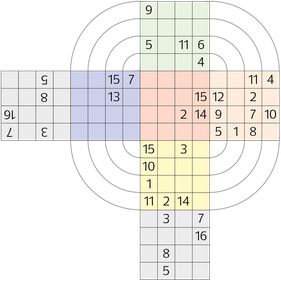
3D-Sudoku
Dies sind die Regeln:
• Jede Seite des Würfels soll die Zahlen 1 bis 16 enthalten.
• Analog zu den Reihen bzw. Spalten des klassischen Sudokus gibt es hier Streifen, die um den Würfel herumlaufen. Insgesamt sind dies zwölf Streifen, je vier für jede der drei
Dimensionen, und jeder Streifen soll die Zahlen 1 bis 16 enthalten.
Dass die graue Würfelseite (sie liegt der roten Würfelseite gegenüber) hier zweimal erscheint, soll für Sie die Lösung komfortabler machen. Der Würfel hat natürlich nur eine graue Seite.
12er-Sudoku
In jeder Zeile, in jeder Spalte und in jedem Unterquadrat (jedes umfasst
12 Kästchen) sollen die Zahlen 1 bis 12 enthalten sein.
Essential 17
Sudokus mit dem Minimum von nur 17 vorgegebenen Zahlen.
Super-Sudoku
In jeder Zeile, in jeder Spalte und in jedem Unterquadrat (jedes umfasst
16 Kästchen) sollen die Zahlen 1 bis 16 enthalten sein.
Monster-Sudoku
In jeder Zeile, in jeder Spalte und in jedem Unterquadrat (jedes umfasst
25 Kästchen) sollen die Zahlen 1 bis 9 sowie die Buchstaben A bis P enthalten sein.
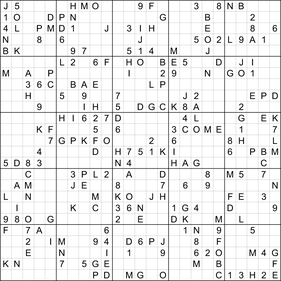
Giganten-Sudoku
Beeindruckende 1296 (in Worten: eintausendzweihundertsechsundneunzig) Kästchen bilden dieses
Rätsel. Wenn Sie Sudoku lieben,
ist unser Giganten-Sudoku die
ultimative Herausforderung für
Sie. Dabei gelten die ganz normalen Sudokuprinzipien: In jeder Zeile, in jeder Spalte und in jedem Unter-
quadrat (jedes umfasst 36 Kästchen) sollen die Zahlen 1 bis 9, die Buch-
staben A bis Z und das Fragezeichen enthalten sein.
Schnitt-Sudoku
Zwei Sudokus, die sich überlagern. Die mittleren drei Blöcken werden vom oberen und vom unteren Sudoku gemeinsam genutzt.
Wortoku
Dieses Buchstaben-Sudoku soll die klassischen Sudoku-Regeln erfüllen, wobei Sie an den jeweiligen Vorgaben erkennen, welche Buchstaben einzusetzen sind. Bei korrekter Lösung erhalten Sie
dabei ein Lösungswort (mit max. neun unterschiedlichen Buchstaben).